Question

The national percentage of automobile accident fatalities that are alcohol related is 39%. In a random sample of 96 automobile accident fatalities in the state of Connecticut, 44 were alcohol related. Is this sufficient evidence to say that Connecticut has a higher percentage of alcohol related automobile fatalities?

Answer 1

Explanation:

Given that:

There are 96 automobile accident fatalities in Connecticut and 44 were alcohol related.

The null hypothesis and the alternative hypothesis for this study can be computed as:

`H_o: P =0.39 \\ \\ H_1:P> 0.39`

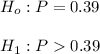
The sample proportion
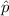`\hat p`= 44/96 = 0.45833

Using the Z formula for a single proportion test, we get;

`Z = \frac{\hat p - P }{\sqrt\frac{{P(1-P)}}{{n}}}`

`Z = \frac{0.45833 - 0.39 }{\sqrt\frac{{0.39(1-0.39)}}{{96}}}`

`Z = \frac{0.06833 }{\sqrt\frac{{0.39(0.61)}}{{96}}}`

`Z =1.37`

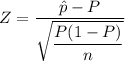
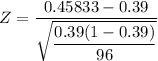
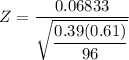
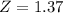
The p-value = 1 -P(Z< 1.37)

The p-value = 1 - 0.9147

The p-value = 0.0853

At the level of significance (∝) 0.05 ;

Since p-value is greater than level of significance (∝); we accept the null hypothesis and conclude that there is no sufficient evidence to say that higher percentage of alcohol is related to automobile fatalities.