Question

There are only 4 mint biscuits and 1 toffee biscuit in a tin. There are only 5 mint sweets and 3 strawberry sweets in a packet. Michaels mum lets him take one biscuit from the tin and one sweet from the packet. Michael takes a biscuit at random from the tin. He also takes a sweet at random from the packet. Work out the probability that either the biscuit is mint, but not both.

Answer 1

0.425

Explanation:

Given that there are 4 mint biscuits and 1 toffee biscuit in a tin and 5 mint sweets and 3 strawberry sweets in a packet.

So, the total number of biscuit in tin = 4+1= 5 and

Number of mint biscuit in tin = 4

Number of toffee biscuit in tin = 1

So, the probability of picking 1 mint biscuit from tin,

`p_1`=(Number of mint biscuit in tin)/(Total number of biscuit in the tin)

`\Rightarrow p_1 =4/5 = 0.8`

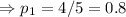
The probability of picking 1 toffee biscuit from tin,

`p_2` =(Number of toffee biscuit in tin)/(Total number of biscuit in the tin)

`\Rightarrow p_2=1/5 = 0.2`

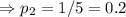
Similarly, the total number of sweets in the basket = 5+3=8 and

Number of mint sweets in the basket = 5

Number of strawberry sweets in the basket = 3

So, the probability of picking 1 mint sweets from the basket,

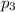`p_3` =(Number of mint sweets in the basket)/(Total number of sweets in the basket)

`\Rightarrow p_3=5/8 = 0.625`

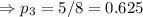
The probability of picking 1 strawberry sweets from the basket

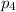`p_4` =(Number of strawberry sweets in the basket)/(Total number of sweets in the basket)

`\Rightarrow p_4=3/8 = 0.375`

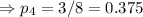
As Michael takes a biscuit from the tin as well as a sweet from the packet randomly, so the possible combinations can be

A) 1 mint biscuit and 1 mint sweets,

B) 1 toffee biscuit and 1 strawberry sweets,

C) 1 mint biscuit and 1 strawberry sweets, and

D) 1 mint sweets and 1 toffee biscuit.

Here, (C) and (D) are the desired case of either the biscuit is mint, but not both.

So, the probability of either the biscuit is mint, but not both

= Probability of ( 1 mint biscuit and 1 strawberry sweets) or (1 mint sweets and 1 toffee biscuit)

`=p_1 * p_4 + p_2* p_3 \\\\=0.8 * 0.375 + 0.2* 0.625 \\\\=0.425`

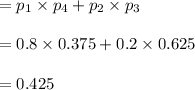
Hence, the probability of either the biscuit is mint, but not both is 0.425