Question:
Triangles PQR and RST are similar right triangles. Which proportion can be used to show that the slope of PR is equal to the slope of RT?
Answer:
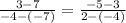
Explanation:
See attachment for complete question
From the attachment, we have that:
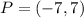

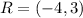
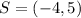

First, we need to calculate the slope (m) of PQR
Here, we consider P and R

Where

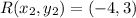
 becomes
becomes
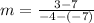 --------- (1)
--------- (1)
Next, we calculate the slope (m) of RST
Here, we consider R and T

Where
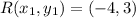
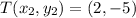
 becomes
becomes
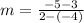 ---------- (2)
---------- (2)
Next, we equate (1) and (2)
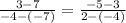
From the list of given options (see attachment), option A answers the question