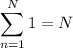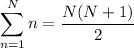The sequence is arithmetic, so there is a constant difference d between consecutive terms such that
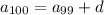
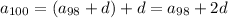
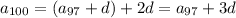
and so on, down to
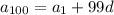
(notice the pattern of 100 = 99 + 1 = 98 + 2 = 97 + 3 = … = 1 + 99)
Solve for d :
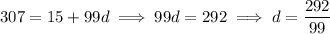
Now, the sum of the first 100 terms of this sequence is
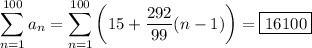
which follows from the well-known sums