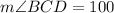Answer:
A. 100 degrees
Explanation:
Given:
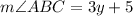
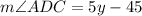
Required:
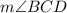
SOLUTION:
✍️First, create an equation that you will use to find the value of y.
 (opposite angles of a parallelogram are congruent to each other)
(opposite angles of a parallelogram are congruent to each other)
 (substitution)
(substitution)
Collect like terms


Divide both sides by -2

✍️Next, find
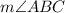 and
and
 .
.
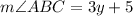
Plug in the value of y
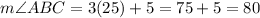
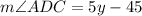
Plug in the value of y

✍️Next, find
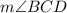 .
.
 (consecutive angles in a parallelogram are supplementary)
(consecutive angles in a parallelogram are supplementary)
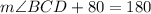 (substitution)
(substitution)
Subtract 80 from each side
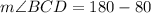
✅