Question

The position of an object at time t is given by s(t) = -8 - 9t. Find the instantaneous velocity at t = 1 by finding the derivative. plz show work

Answer 1

The instantaneous velocity at t = 1 will be:

• 
  `(d)/(dt)\left(-8-9t\right)=-9`

Explanation:

Given the position of an object at a time
`t`

`s\left(t\right)=-8-9t`

As we know that determining the derivative of the position function with respect to time t would give us the instantaneous velocity, so

`(ds)/(dt)=(d)/(dt)\left(-8-9t\right)`

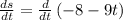
Applying the sum/difference rule:

`\left(f\pm g\right)'=f\:'\pm g'`

`(ds)/(dt)=-(d)/(dt)\left(8\right)-(d)/(dt)\left(9t\right)`

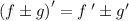
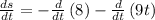
as

`(d)/(dt)\left(8\right)=0` ∵
`(d)/(dx)\left(a\right)=0`

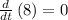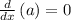
and

`(d)/(dt)\left(9t\right)=9` ∵
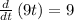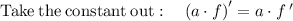`\mathrm{Take\:the\:constant\:out}:\quad \left(a\cdot f\right)'=a\cdot f\:'` and
`(d)/(dt)\left(t\right)=1`

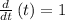
so the expression becomes

`(ds)/(dt)=-(d)/(dt)\left(8\right)-(d)/(dt)\left(9t\right)`

`=-0-9`

`=-9`

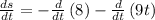
As the derivative is constant.

Therefore, the instantaneous velocity at t = 1 will be:

• 
  `(d)/(dt)\left(-8-9t\right)=-9`