Answer:
tarro corto
Explanation:
Aquí tenemos que comprar el frasco que tiene el menor costo por volumen.
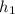 = Altura del frasco corto
= Altura del frasco corto
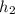 = La altura del frasco alto es el doble que el del frasco corto. =
= La altura del frasco alto es el doble que el del frasco corto. =
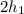
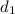 = Diámetro del frasco corto
= Diámetro del frasco corto
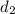 = El diámetro del frasco alto es la mitad del frasco corto =
= El diámetro del frasco alto es la mitad del frasco corto =
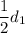
El volumen de un cilindro es
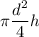
La razón de los volúmenes de los frascos es
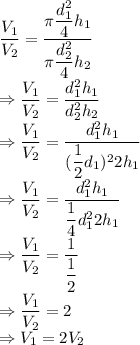
El costo del frasco corto por unidad de volumen es
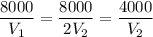
El costo del frasco alto por unidad de volumen es
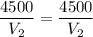
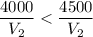
Entonces, el costo del frasco corto por unidad de volumen es menor que el costo por unidad de volumen del frasco alto.
Por lo tanto, deberíamos tomar el frasco corto.