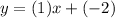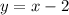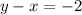Question

(-5,-7) and (3,1)

write equation in point slope form, intercept form, and standard form

Answer 1

Please check the explanation

Explanation:

Given the points

• (-5,-7)

• (3,1)

Determining the slope between the points:

`\mathrm{Slope}=(y_2-y_1)/(x_2-x_1)`

`\left(x_1,\:y_1\right)=\left(-5,\:-7\right),\:\left(x_2,\:y_2\right)=\left(3,\:1\right)`

`m=(1-\left(-7\right))/(3-\left(-5\right))`

`m=1`

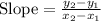
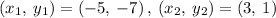
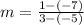
Writing the equation in point-slope form

As the point-slope form of the line equation is defined by

`y-y_1=m\left(x-x_1\right)`

Putting the point
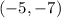`(-5,-7)` and the slope
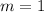`m = 1` in the line equation

`y-y_1=m\left(x-x_1\right)`

`y-\left(-7\right)=1\left(x-\left(-5\right)\right)\\`

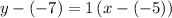
Hence, the equation in the point-slope form will be:

`y-\left(-7\right)=1\left(x-\left(-5\right)\right)`

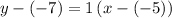
Writing the equation in slope-intercept form

As the point-slope of the equation is

`y=mx+b`

where m is the slope and b is the y-intercept

Putting m = 1 and (3, 1) to determine the y-intercept

`y = mx+b`

`1 = 1 (3) + b`

`1 = 3 + b`

`b = -2`

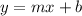
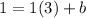
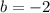
so putting
`b=-2` and m = 1 in the slope-intercept form

`y = mx+b`

`y = (1)x + (-2)`

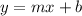
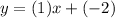
Therefore, the equation in slope-intercept form is:

`y = x -2`

Writing the equation in the standard form form

As we know that the equation in the standard form is

`Ax+By=C`

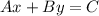
where x and y are variables and A, B and C are constants

As we already know the equation in slope-intercept form

`y = (1)x + (-2)`

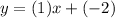
so just simplify the equation to write in standard form

`y = (1)x + (-2)`

`y = x - 2`

`y - x = -2`