Question

Find sin A and cos A

A) sin A = 3/5; cos A = 4/5
B) sin A = 4/5; cos A = 3/5
C) sin A = 5/4; cos A = 4/5
D) sin A = 4/3; cos A = 3/4

Answer 1

B

Explanation:

sinA=opp/hyp

sinA=16/20=4/5

cosA=adj/hyp

cosA=12/20=3/5

Answer 2

We found sinA= 3/5 and cosA=4/5

Option A is correct.

Explanation:

The formula to find sin A is :

`sin A = (Perpendicular)/(Hypotenuse)`

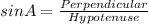
while the formula to find cos A is:

`cosA=(Base)/(Hypotenuse)`

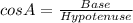
So, in the figure given:

Base = 16

Perpendicular = 12

Hypotenuse = 20

Now, finding sin A and cos A using formulas and above values

`sin A = (Perpendicular)/(Hypotenuse)\\sin A = (12)/(20)\\sinA=(3)/(5)`

`cosA=(Base)/(Hypotenuse)\\cosA=(16)/(20)\\cosA=(4)/(5)`

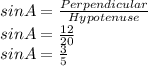
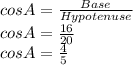
So, we found sinA= 3/5 and cosA=4/5

Option A is correct.