Answer:
Approximately
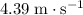 (assuming that
(assuming that
 .)
.)
Step-by-step explanation:
Let the initial velocity of this stone be
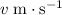 (
(
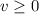 because speed should be non-negative.) That should be numerically equal to the initial horizontal speed of this stone. Because the stone was thrown horizontally, its vertical speed would initially be zero (
because speed should be non-negative.) That should be numerically equal to the initial horizontal speed of this stone. Because the stone was thrown horizontally, its vertical speed would initially be zero (
 .)
.)
The weight of this stone will accelerate the stone downwards. Because the weight of the stone is in the vertical direction, it will have no effect on the horizontal speed of the stone.
Therefore, if air resistance is indeed negligible, the horizontal speed of this stone will stay the same. The horizontal speed of the stone after
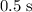 should still be
should still be
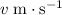 - same as its initial value.
- same as its initial value.
On the other hand, if
 , the (downward) vertical speed of this stone will increase by
, the (downward) vertical speed of this stone will increase by
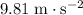 every second. After
every second. After
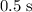 , the vertical speed of this stone would have become:
, the vertical speed of this stone would have become:
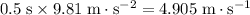 .
.
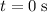 :
:
- Horizontal speed:
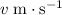 .
. - Vertical speed:
 .
.
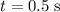 :
:
- Horizontal speed:
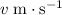 .
. - Vertical speed:
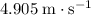 .
.
Refer to the diagram attached. Consider the vertical speed and the horizontal speed of this rock as lengths of the two legs of a right triangle. The numerical value of the velocity of this stone would correspond to the length of the hypotenuse of that right triangle. Apply the Pythagorean Theorem to find that numerical value:
 .
.
At
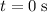 , the magnitude of the velocity of this stone would be
, the magnitude of the velocity of this stone would be
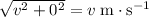 .
.
At
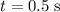 , the magnitude of the velocity of this stone would be
, the magnitude of the velocity of this stone would be
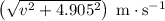 .
.
The question requires that the magnitude of the velocity of the stone at
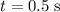 should be
should be
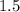 times the value at
times the value at
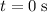 . In other words:
. In other words:
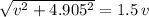 .
.
Square both sides of this equation and solve for
 :
:
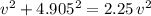 .
.
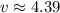 (
(
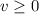 given that speed should be non-negative.)
given that speed should be non-negative.)
Therefore, the initial velocity of this stone should be approximately
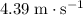 .
.