Question

Helppp quick enough points

Answer 1

2a)

To verify, set the factors to zero.

(x - 2) = 0, x = 2

(x + 3) = 0, x = -3

Insert zero's in the equation:

when x = 2

3(2)³ + 2(2)² - 19(2) + 6 = 0

when x = -3

3(-3)³ + 2(-3)² - 19(-3) + 6 = 0

Hence verified the factors.

2b)

`= \sf (\left(3x^3+2x^2-19x+6\right))/(\left(x-2\right)\left(x+3\right))`

`\sf = (\left(3x-1\right)\left(x-2\right)\left(x+3\right))/(\left(x-2\right)\left(x+3\right))`

`\sf = 3x -1`

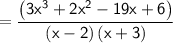
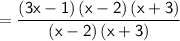
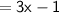
The remaining factor is (3x - 1)

2c)

Set the factors to zero to find real zeros of f

• (3x - 1) = 0, x = 1/3

• (x - 2) = 0, x = 2

• (x + 3) = 0, x = -3

2d)

Complete factorization: (3x - 1)(x - 2)(x + 3)