Question

Write a linear function f with the values f (6) = 8 and f (9) = 3.

Answer 1

Given:

Two values of a linear function are f (6) = 8 and f (9) = 3.

To find:

The linear function.

Solution:

According to the question f (6) = 8 and f (9) = 3, it means the function passes through (6,8) and (9,3).

If a linear function passes through two points then the equation is

`y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)`

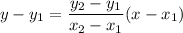
So, the equation of linear function is

`y-8=(3-8)/(9-6)(x-6)`

`y-8=(-5)/(3)(x-6)`

`y-8=-(5)/(3)(x)-(5)/(3)(-6)`

`y-8=-(5)/(3)(x)+10`

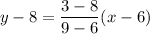
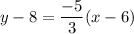
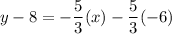
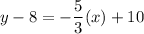
Add 8 on both sides.

`y=-(5)/(3)(x)+10+8`

`y=-(5)/(3)(x)+18`

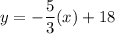
Function form is,

`f(x)=-(5)/(3)(x)+18`

Therefore, the required linear function is
`f(x)=-(5)/(3)(x)+18`.