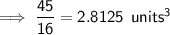Answer:
Part A
To find the number of cubes that can be packed into the rectangular prism, calculate the volume of the rectangular prism and the volume of the cube, then divide the volume of the prism by the volume of the cube.

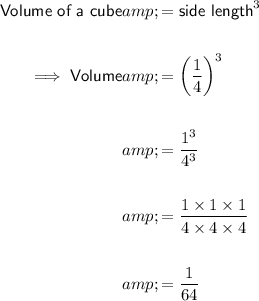

Part B
Convert the sides lengths of the rectangular prism into improper fractions with 4 as the denominator:
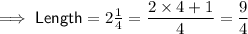
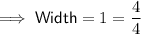
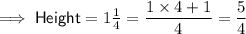
As the side lengths of the cube are 1/4 then the volume of the prism in terms of the small cube is:
⇒ 9 x 4 x 5 = 180 units³
Using the found volume of the prism from part A, the volume of the rectangular prism in terms of a unit cube is: