Question

Find an equation for the perpendicular bisector of the line segment whose endpoints are (−3,4) and (−7,−6).

Answer 1

She's right, praise jeebus :3

Explanation:

Answer 2

`y=-(2)/(5)x-3`

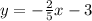
Explanation:

First, you must find the midpoint of the segment, the formula for which is
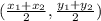`((x_(1)+x_(2))/(2),(y_(1)+y_(2))/(2))`. This gives you (-5,-1) as the midpoint. This is the point at which the segment will be bisected.

Next, since we are finding a perpendicular bisector, we must determine what slope is perpendicular to that of the existing segment. To determine the segment's slope, we use the slope formula
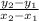`(y_(2)-y_(1) )/(x_(2)-x_(1))`, which gives us a slope of
`(5)/(2)`.

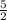Perpendicular lines have opposite and reciprocal slopes. The opposite reciprocal of
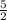`(5)/(2)` is
`-(2)/(5)`.

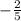We now know that the perpendicular travels through the point (-5,-1) and has a slope of
`-(2)/(5)`.

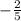Solve for
`b` in
`y=mx+b`.

`y=mx+b\\-1=-(2)/(5)(-5)+b\\-1=2+b\\-3=b\\b=-3`

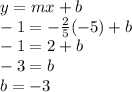
Therefore, the equation of the perpendicular bisector is
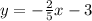`y=-(2)/(5)x-3`.