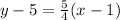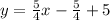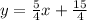Question

Determine the equation of the perpendicular bisector JK whose endpoints are J(-4,9) and K(6,1). Show all your work below. (Use of the grid is optional.)​

Answer 1

`y=(5)/(4)x+(15)/(4)`

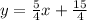
Explanation:

Coordinates of segment with endpoints J and K are,

J(-4, 9) and K(6, 1)

Midpoint of the segment JK =
`((x_1+x_2)/(2),(y_1+y_2)/(2))`

=
`((-4+6)/(2),(9+1)/(2))`

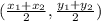
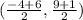
= (1, 5)

Slope of JK,
`(m_1)=(y_2-y_1)/(x_2-x_1)`

=
`(9-1)/(-4-6)`

=
`-(4)/(5)`

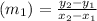
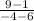
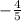
Let the equation of perpendicular bisector passing through
`(x_1,y_1)` and slope
`m_2` is,

`y-y_1=m_2(x - x_1)`

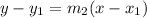
By the property of perpendicular lines,

`m_1* m_2=-1`

`-(4)/(5)* m_2=-1`

`m_2=(5)/(4)`

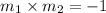
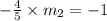
Therefore, equation of the line passing through midpoint (1, 5) and slope =
`(5)/(4)` will be,

`y-5=(5)/(4)(x-1)`

`y=(5)/(4)x-(5)/(4)+5`

`y=(5)/(4)x+(15)/(4)`