Question

You have a garden in your backyard that measures 15 meters by 20 meters. You want to place stepping stones around the perimeter of the garden. The area of the new garden (original garden + stone placed around the perimeter) is 336m². What is the width of the stone border? (Assume the border has the same width around the entire perimeter.) Equation used = bi Width of stone border = meters​

Answer 1

0.5 m

Explanation:

Given that the dimensions of the garden are 15 meters by 20 meters.

The area of the new garden (original garden + stone placed around the perimeter) is 336m².

Let d be the width of the border having stepping stones as shown in the figure. The shaded region in the figure is the area having stepping stones.

The area including the shaded region
`= (15+2d)(20+2d) m^2`

`\Rightarrow 336 = (15+2d)(20+2d) \\\\\Rightarrow 336 = 300+ 70 d +4d^2 \\\\\Rightarrow 4d^2 +70d+300-336=0 \\\\\Rightarrow 4d^2 +70d-36=0 \\\\\Rightarrow 2d^2 +35d-18=0 \\\\\Rightarrow 2d^2 +36d-d-18=0 \\\\\Rightarrow (2d-1)(d+18)=0 \\\\\Rightarrow (2d-1)=0, \; or \; (d+18) \\\\\Rightarrow d= 0.5\;or -18 \\\\`

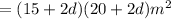
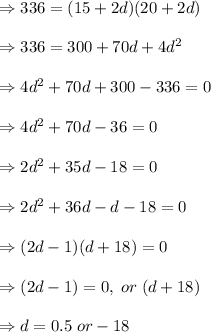
As the width of the stone border can't be a negative value, so taking the positive value.

Hence, the width of the stone border is 0.5 m.

So, the wi