The derivative of a function f(x) is defined as the limit,

With f(x) = x⁶, we have
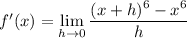
Expand f(x + h) in the numerator:
(x + h)⁶ = x⁶ + 6x⁵h + 15x⁴h² + 20x³h³ + 15x²h⁴ + 6xh⁵ + h⁶
so that the x⁶ terms cancel, leaving us with

h is approaching 0, so h ≠ 0 and we can cancel the common factor in the numerator and denominator:
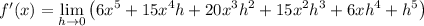
Now as h converges to 0, each term containing h vanishes, leaving us with
f'(x) = 6x⁵