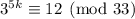First, 27 = 3³, so 27¹⁵ = (3³)¹⁵ = 3⁴⁵.
So we have
27¹⁵ ≡ 3⁴⁵ (mod 33)
and
3 ≡ 3 (mod 33)
3² ≡ 9 (mod 33)
3³ ≡ 27 (mod 33)
3⁴ ≡ 81 ≡ 15 (mod 33)
3⁵ ≡ 3 • 15 ≡ 45 ≡ 12 (mod 33)
From here, the cycle continues:
3⁶ ≡ 3 • 12 ≡ 36 ≡ 3 (mod 33)
3⁷ ≡ 3 • 3 ≡ 9 (mod 33)
and so on.
This is to say that, for each power of 3, where the power is a multiple of 5, the remainder will always be 12, i.e. for any positive integer k,