Answer:
The result of adding the two equations is:
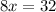
And the solution to the system is (4, 6).
Explanation:
We are given the system of equations:
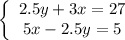
We can solve by elimination. If we add the two equations together, we acquire:

Simplifying yields:
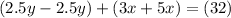
Combine like terms. Therefore, we the two equations are added together, we obtain:
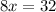
Solve for x by dividing both sides by 8:
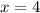
With the value of x, we can solve for y. Using the first equation:
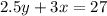
Substitute 4 for x and solve for y:
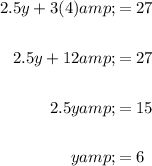
In conclusion, our solution to the system is (4, 6).