Answer:
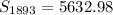
Explanation:
The correct form of the question is:
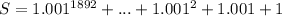
Required
Solve for Sum of the sequence
The above sequence represents sum of Geometric Sequence and will be solved using:
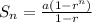
But first, we need to get the number of terms in the sequence using:
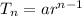
Where
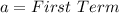
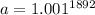
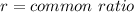
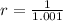
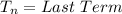
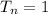
So, we have:
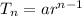
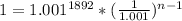
Apply law of indices:
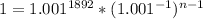
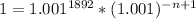
Apply law of indices:
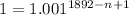
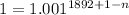
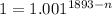
Represent 1 as
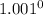
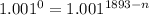
They have the same base:
So, we have
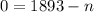
Solve for n
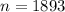
So, there are 1893 terms in the sequence given.
Solving further:
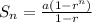
Where
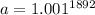
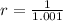
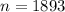
So, we have:
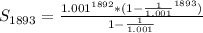
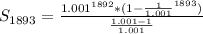
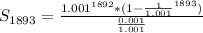
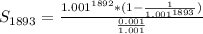
Simplify the numerator
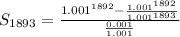
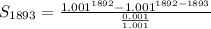
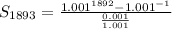
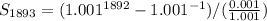
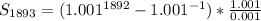
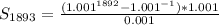
Open Bracket
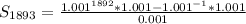
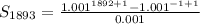
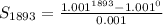
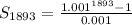
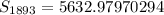
Hence, the sum of the sequence is:
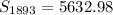 ----- approximated
----- approximated