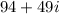Answer:
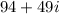
Explanation:
Given
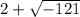 and
and
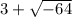
Required
Determine the products
We have:
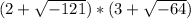
Factorize:
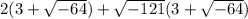
Open Brackets
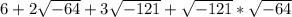
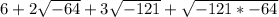
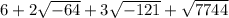
Expand the expression in square roots
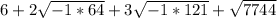
Split roots
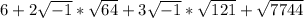
Take positive square roots of 64, 121 and 7744
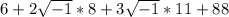
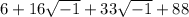
Collect Like Terms
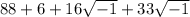
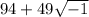
A complex number in standard form is:
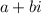
Where
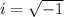
So:
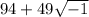
=
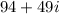
Hence:
The product of
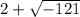 and
and
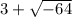 is
is