Answer:
The length of side of largest square is 15 inches
Explanation:
The given suares are when joined in the way as shown in picture their sides form a right agnled triangle.
Area of square 1 and perimeter of square 2 will be used to calculate the sides of the triangle.
So,
Area of square 1: 81 square inches
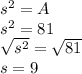
Perimeter of square 2: 48 inches
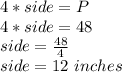
We can see that a right angled triangle is formed.
Here
Base = 12 inches
Perpendicular = 9 inches
And the side of largest square will be hypotenuse.
Pythagoras theorem can be used to find the length.
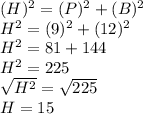
Hence,
The length of side of largest square is 15 inches