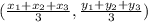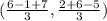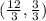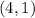Question

Find the Centroid of AABC if A (6, 2), B (-1, 6) and C (7, -5).

Answer 1

Centroid of the triangle is (4, 1).

Explanation:

Centroid Formula (for a triangle)

`\text{centroid} = ((x_1 + x_2 + x_3)/(3), (y_1 + y_2 + y_3)/(3))`
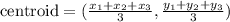
x₁, x₂, x₃ ... x-coordinates of the vertices

y₁, y₂, y₃ ... y-coordinates of the vertices

Given:

A(6, 2)

B(-1, 6)

C(7, -5)

Insert coordinates in the formula. Points are in form (x, y).

`((x_1 + x_2 + x_3)/(3), (y_1 + y_2 + y_3)/(3))`

`((6 - 1 + 7)/(3), (2 + 6 - 5)/(3))`

`((12)/(3), (3)/(3))`

`(4, 1)`