Find the graph of the equation y = x² - 4x + 4.
This is in the general form y = ax² + bx + c
1.) Graph shape. For parabolas, if the a-value is positive, the graph opens upward, creating a U-shaped graph. If the a-value is negative, the graph will open downwards.
Our equation has a positive a-value, which means our graph will open upwards in a U shape. This rules out options (a) and (d), as they both open downwards.
2.) The axis of symmetry. To find the axis of symmetry (the middle of the graph, and in this case, its x-coordinate), use the formula
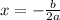 .
.
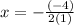

The vertex of the graph is at x = 2. Graphs (b) and (d) both have a vertex at x = 2, but we already ruled out (d) because it opens in the wrong direction for our equation. This means the correct option must be option (b).
Note: The equation of the parabola tells us that the y-intercept of the graph is at y = 4. We can see that option (b) is the only option that has a y-int at 4. This allows us to check our work.