Question

PLEASE HELP< ILL GIVE 45 POINTS AFTER YOU ANSWER!!!

△XYZ is translated up 3 units to form the image ∆X′Y′Z′.

What are the coordinates of the vertices of ∆X′Y′Z′ ?

Enter your answer by filling in the boxes.

X′ =

Y′ =

Z′ =


Picture:

A right triangle on a grid with a range from negative eight to eight on the x and y axis whose coordinates are negative four comma six for point X, six comma one for point Y, and one comma one for point Z on a grid

Answer 1

Given:

Vertices of △XYZ are X(-4,6), Y(6,1) and Z(1,1).

To find:

The vertices of ∆X′Y′Z′.

Solution:

According to the question, △XYZ is translated 3 units up to form the image ∆X′Y′Z′, so rule of translation is defined as

`(x,y)\to (x,y+3)`

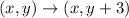
Now,

`X(-4,6)\to X'(-4,6+3)`

`X(-4,6)\to X'(-4,9)`

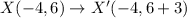
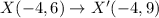
Similarly,

`Y(6,1)\to Y'(6,1+3)`

`Y(6,1)\to Y'(6,4)`

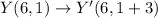
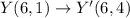
and,

`Z(1,1)\to Z'(1,1+3)`

`Z(1,1)\to Z'(1,4)`

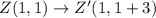
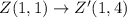
Therefore,
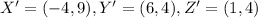`X'=(-4,9),Y'=(6,4),Z'=(1,4)`.