Question

Among 2450 randomly selected male car occupants over the age of​ 8, 76​% wear seatbelts. Among 2900 randomly selected female car occupants over the age of​ 8, ​74% wear seat belts. Use a 0.1 significance level to test the claim that both genders have the same rate of seat belt use. Does there appear to be a gender​ gap?

a. There appears to be a gender gap because there is not a significant difference in the proportions.
b. There does not appear to be a gender gap because there is a significant difference in the proportions.
c. There does not appear to be a gender gap because there is not a significant difference in the proportions.
d. There appears to be a gender gap because there is a significant difference in the proportions.

Answer 1

The correct option is D

Explanation:

From the question we are told that

The sample size for male car occupant is
`n_1 = 2450`

The number that wear seat belt is
`k_1 = (76)/(100) * 2450 = 1862`

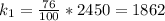
The sample size for female car occupant is
`n_2 = 2900`

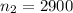
The number that wear a seat belt is
`k_2 = (74)/(100) * 2900 = 2146`

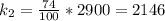
Generally the population proportion is mathematically represented as

`p = (x_1 + x_2 )/(n_1 + n_2 )`

=>
`p = (1862 + 2146 )/(2450 + 2900 )`

=>
`p = 0.7492`

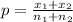
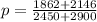
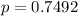
The sample proportion for male car occupant is

`\^ p_1 = (k_1)/(n_1)`

=>
`\^ p_1 = (1862)/(2450)`

=>
`\^ p_1 = 0.76`

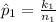
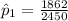
The sample proportion for female car occupant is

`\^ p_2 = (k_2)/(n_2)`

=>
`\^ p_2 = (2146)/(2900)`

=>
`\^ p_1 = 0.74`

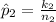
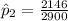
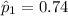
The null hypothesis is
`H_o : p_1 = p_2`

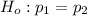
The alternative hypothesis is
`H_a : p_1 \\e p_2`

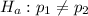
Generally the standard error is mathematically represented as

`SE = \sqrt{(p(1 -p ))/( n_1 + n_2) }`

=>
`SE = \sqrt{(0.7492 (1 -0.7492 ))/( 2450 + 2900) }`

=>
`SE = 0.005926`

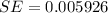
Generally the test statistics is mathematically represented as

`z = (\^ p_1 - \^ p_2)/(SE)`

=>
`z = (0.76 -0.74)/(0.005926)`

=>
`z = 3.37`

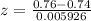
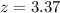
From the z table the area under the normal curve to the right corresponding to 3.37 is

`P(Z > 3.37) = 0.00037584`

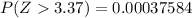
Generally the p-value is mathematically represented as

`p-value = 2 * P(Z > 3.37)= 2* 0.00037584 = 0.0007 5`

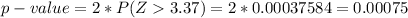
From the value obtained we see that
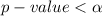`p-value < \alpha` hence

The decision rule is

Reject the null hypothesis

The conclusion is

There appears to be a gender gap because there is a significant difference in the proportions