Question

What is the magnitude of the angular momentum (in kgm2/s) of a 40 g golf ball flying through the air and spinning at 4300 rpm after having been hit? The golf ball can be modelled as a uniformly dense sphere with a radius of 2.5 cm.

Answer 1

`L=0.0045\ kg-m^2/s`

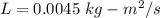
Step-by-step explanation:

Given that,

The mass of a golf ball, m = 40 g = 0.04 kg

Its angular velocity,
`\omega=4300\ rpm=450.29\ rad/s`

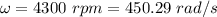
The radius of the sphere is 2.5 cm or 0.025 m

We need to find the magnitude of the angular momentum of the ball. It is given by the formula as follows:

`L=I\omega`

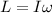
Where I is moment of inertia

For sphere,
`I=(2)/(5)mr^2`

`L=(2)/(5)mr^2\omega\\\\L=(2)/(5)* 0.04* (0.025)^2* 450.29\\\\L=0.0045\ kg-m^2/s`

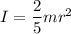
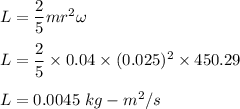
So, the magnitude of the angular momentum of the sphere is
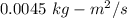`0.0045\ kg-m^2/s`.