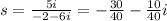Answer:
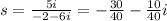
Explanation:
We have the following complex number
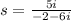 , we proceed to simplify the expression as follows:
, we proceed to simplify the expression as follows:
1)
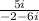 Given.
Given.
2)
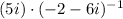 Definition of division.
Definition of division.
3)
![[(5i)\cdot (-2-6i)^(-1)]\cdot [(-2+6i)\cdot (-2+6i)^(-1)]](https://img.qammunity.org/2021/formulas/mathematics/high-school/fhbmgy8fq3h2gfgmr4tq2dfe12bq5n0rxh.png) Modulative and associative properties/Existence of the additive inverser
Modulative and associative properties/Existence of the additive inverser
4)
![[(5i)\cdot (-2+6i)]\cdot [(-2-6i)^(-1)\cdot (-2+6i)^(-1)]](https://img.qammunity.org/2021/formulas/mathematics/high-school/jvwnwddr9chaqgxzf0imombf562fu745iv.png) Commutative and associative properties.
Commutative and associative properties.
5)
![[(5i)\cdot (-2+6i)]\cdot [(-2-6i)\cdot (-2+6i)]^(-1)](https://img.qammunity.org/2021/formulas/mathematics/high-school/aewi6tougcucaa4oq2ei4vks02yskfhu86.png)

6)
![[(5i)\cdot (-2+6i)]\cdot [4+36]^(-1)](https://img.qammunity.org/2021/formulas/mathematics/high-school/tgqojnp2a9yx9hhkuc5vcufwz0hgxclbf5.png)
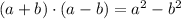 /Definition of complex number/
/Definition of complex number/
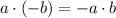
7)
![[(5i)\cdot (-2)+(5i)\cdot (6i)]\cdot 40^(-1)](https://img.qammunity.org/2021/formulas/mathematics/high-school/iijdy2l9nx2952lcy29dfpsdwr2bfwj3v6.png) Definition of sum.
Definition of sum.
8)
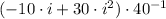
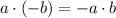 /Associative and commutative properties.
/Associative and commutative properties.
9)
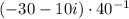 Commutative properties/Definition of complex number/
Commutative properties/Definition of complex number/
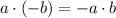
10)
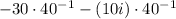 Distributive property.
Distributive property.
11)
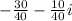 Definition of division/Result.
Definition of division/Result.