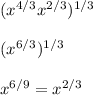Question

Which expression is equivalent to (x^4/3 x^2/3) ^1/3

Answer 1

`x^(\tfrac 23)`

Step by step explanation:

`\left(x^(\tfrac 43) \cdot x^(\tfrac 23) \right)^(\tfrac 13)\\\\\\=\left(x^(\tfrac 43 + \tfrac 23) \right)^(\tfrac 13)\\\\\\=\left(x^(\tfrac 63) \right)^(\tfrac 13)\\\\\\=\left(x^2 \right)^(\tfrac 13)\\\\\\=x^(\tfrac 23)`

Answer 2

`x^(2/3)`

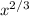
Explanation:

When two terms with the same base are directly next to each other (being multiplied), the powers are added. When a term raised to a power is raised to another power, the powers are multiplied.

Begin by adding (4/3) and (2/3) to get (6/3). Then, multiply (6/3) by (1/3) to get (6/9). This number can be simplified to (2/3).

`(x^(4/3)x^(2/3) )^(1/3) \\\\(x^(6/3))^(1/3)\\\\x^(6/9) = x^(2/3)`