Solution :
The sun emits =
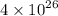 J of energy per second
J of energy per second
=
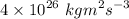
We know,
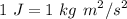
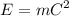 , where C =
, where C =

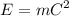
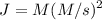
Dividing both sides by 1 second
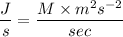
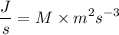
Then,
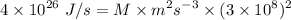
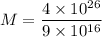
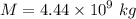
Now according to the information, 99.3% hydrogen.
If 0.7 % of hydrogen produce =
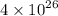 J of energy per second
J of energy per second
Then 1% of hydrogen will produce =
 J energy per second
J energy per second
So, 100% of hydrogen will produce =
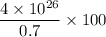 J energy per second
J energy per second
=
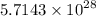 J energy per second
J energy per second
Mass of hydrogen undergo fusion in sun per second
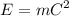
Similarly,
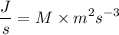
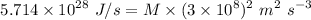
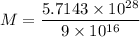 kg
kg
 kg
kg