Question

Professor Gersch grades his exams and sees that the grades are normally distributed with a mean of 77 and a standard deviation of 6.Based on the Empirical Rule, between what two grades should you expect to find roughly the middle 95% of the distribution?a. 65 to 89b. 77 to 83c. 71 to 83d. 77 to 89e. 59 to 95

Answer 1

The correct option is a. 65 to 89.

Explanation:

According to the Empirical Rule in a normal distribution with mean µ and standard-deviation σ, nearly all the data will fall within 3 standard deviations of the mean. The empirical rule can be broken into three parts:

• 68% data falls within 1 standard deviation of the mean. That is P (µ-σ≤X≤ µ+σ) = 0.68.

• 95% data falls within 2 standard deviations of the mean. That is P (µ-2σ≤X≤ µ+2σ) = 0.95.

• 99.7% data falls within 3 standard deviations of the mean. That is P (µ-3σ≤X≤ µ+3σ) = 0.997.

The information provided is:

`\mu=77\\\sigma = 6`

Use the Empirical rule to compute the middle 95% of the distribution as follows:

`P(\mu-2\sigma\leq X\leq \mu+2\sigma)=0.95\\\\\mu-2\sigma=77-(2* 6)=65\\\\\mu+2\sigma=77+(2* 6)=89\\\\\Rightarrow P(65\leq X\leq 89)=0.95`

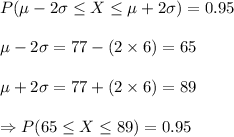
Thus, the correct option is a. 65 to 89.