Answer:
Why might he think that and what would you tell him?
He thought perhaps that numbers were formed by rational numbers of the form
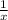 , where
, where
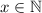 . I would tell him that there are rational numbers
. I would tell him that there are rational numbers
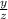 , such that
, such that
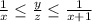 , where
, where
 ,
,
 ,
,
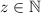 .
.
Is there a number that falls between these?
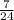 is a rational number between
is a rational number between
 and
and
 .
.
Explanation:
Why might he think that and what would you tell him?
He thought perhaps that numbers were formed by rational numbers of the form
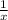 , where
, where
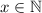 . I would tell him that there are rational numbers
. I would tell him that there are rational numbers
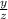 , such that
, such that
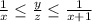 , where
, where
 ,
,
 ,
,
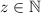 .
.
Is there a number that falls between these?
Indeed, the average number of
 and
and
 , for instance. That is:
, for instance. That is:

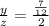
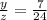
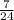 is a rational number between
is a rational number between
 and
and
 .
.