Answer:
Explained below.
Explanation:
(1)
The confidence level is, 91%.
Compute the value of α as follows:
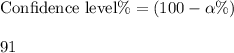
(2)
As the population standard deviation is provided, i.e. σ = 256 psi, the z value would be appropriate.
The z value for α = 0.09 is,
z = 1.69
(3)
Compute the 91% confidence interval as follows:
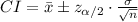

(4)
The 91% confidence interval for population mean implies that there is a 0.91 probability that the true value of the mean is included in the interval, (2942.29, 3057.71) psi.