Question

Write the following expression in algebraic form.

cos(arcsin 3x)

Answer 1

Explanation:

If we consider a triangle with the length of the hypotenuse being equal to 1 and the length of the opposite side = 3x.

However, recall that in a right-angle triangle;

SIne = opposite/hypothenuse

Thus; let the angle facing the opposite be y

Then;

SIn y = 3x/1

Sin y = 3x

Thus, y = arcsin (3x)

Now; to find cos(arcsin 3x)

Recall that:

Cosine = adjacent/hypotenuse

Now, using Pythagoras rule;

`\mathsf{Adjacent \ side = √((hypotenuse)^2 -(opposite^2))}`

`\mathsf{Adjacent \ side = √((1)^2 -(3x^2))}`

`\mathsf{Adjacent \ side = √(1 -9x^2)}`

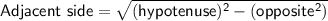
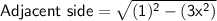
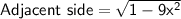
cos(arcsin 3x) = cos y = adjacent side/hypotenuse =
`(√(1 -9x^2))/(1)`

cos(arcsin 3x) =
`(√(1 -9x^2))/(1)`