Answer:
a
i. Proportion
b
Best point estimate is

c
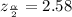
d
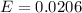
e

Explanation:
From the question we are told that
The sample size is n = 3765
The proportion that feel the businesses in Laradise, are run by compliant individuals is

Considering question a
The correct option is Proportion because in the prompt we are told to obtain the fraction of the total sample size that has a particular attribute (which their opinion of business in Laradise) and this is what a proportion represents
Considering question b
The best point estimate is
 because this proportion best defines the fraction of the sample size who feel the businesses in Laradise, are run by compliant individuals
because this proportion best defines the fraction of the sample size who feel the businesses in Laradise, are run by compliant individuals
Considering question c
Generally given that the sample size is large enough n > 30 , it then means that the distribution is approximately normal so
From the question we are told the confidence level is 99% , hence the level of significance is
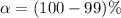
=>

Generally from the normal distribution table the critical value of
 is
is
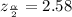
Considering question d
Generally the margin of error is mathematically represented as

=>

=>
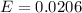
Considering question e
Generally 99% confidence interval is mathematically represented as
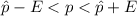
=>
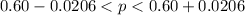
=>
