Question

A 72.0-kg person pushes on a small doorknob with a force of 5.00 N perpendicular to the surface of the door. The doorknob is located 0.800 m from axis of the frictionless hinges of the door. The door begins to rotate with an angular acceleration of 2.00 rad/s2, What is the moment of inertia of the door about the hinges? A) 2.74 kg m2 B) 1.88 kg m2 C) 0.684 kg m2 D) 4.28 kg m2 E) 7.52 kg m2

Answer 1

`I=2\ kgm^2`

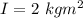
Step-by-step explanation:

Given that,

Mass of a person, m = 72 kg

Force acting on a doorknob, F = 5 N

The doorknob is located 0.800 m from axis of the frictionless hinges of the door.

The angular acceleration of the dor, a = 2 rad/s²

We need to find the moment of inertia of the door about the hinges.

The person applies a torque to the door and it is given by :

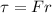`\tau=Fr` ...(1)

Also, the torque is equal to :

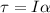`\tau=I\alpha` ...(2)

From equation (1) and (2) we get :

`Fr=I\alpha`

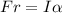
I is the moment of inertia

`I=(Fr)/(\alpha )\\\\I=(5* 0.8)/(2)\\\\=2\ kgm^2`

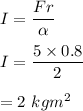
So, the moment of inertia of the door about the hinges is
`2\ kgm^2`.