Question

Tom the turkey is 2.5 feet tall and he casts a shadow that is 4 feet. The Thanksgiving Parade float version of Tom is 14 feet tall. How long is the shadow of the parade float?

Answer 1

22.4 ft

Explanation:

Given

`Height = 2.5ft`

`Shadow = 4ft`

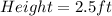
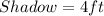
Required

Determine the shadow of 14 ft Tom

The given parameters represents direct variation.

Let x represents the shadow of Tom.

So, we have:

When

`2.5ft\ height = 4ft\ Shadow`

`14ft\ height = x`

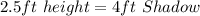
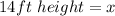
Cross Multiply:

`2.5 * x = 14 * 4`

`2.5 * x = 56`

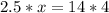
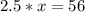
Solve for x

`x = 56/2.5`

`x = 22.4`

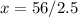
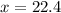
Hence, the height of the shadow is 22.4ft