Answer:
The coordinates of A' are
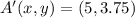 .
.
The coordinates of B' are
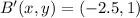 .
.
The coordinates of C' are
 .
.
Explanation:
The statement is incomplete, we present the complete statement below: Triangle ABC is dilated using the dilation rule
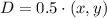 to form triangle A’B’C’. Point A is located at
to form triangle A’B’C’. Point A is located at
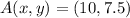 , point B is located at
, point B is located at
 , and point C is located at
, and point C is located at
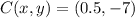 . What are the coordinates of A’? What are the coordinates of B’? What are the coordinates of C’?
. What are the coordinates of A’? What are the coordinates of B’? What are the coordinates of C’?
We proceed to calcultate the coordinates of the triangle A'B'C' hereafter:
What are the coordinates of A'?
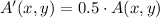 (1)
(1)

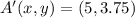
The coordinates of A' are
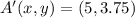 .
.
What are the coordinates of B'?
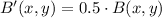 (2)
(2)
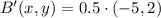
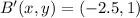
The coordinates of B' are
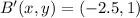 .
.
What are the coordinates of C'?
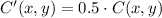 (3)
(3)
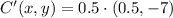

The coordinates of C' are
 .
.