Question

A chain of retail computer stores opened 2 stores in its first year of operation. After 8 years of operation, the chain consisted of 206 stores. If the number of stores opening per year is increasing at an exponential rate, identify the continuous rate of growth. Round k to the nearest hundredth. *

Answer 1

0.66

Explanation:

The exponential growth equation is expressed as;

S(t) = S0e^kt

S(t) is the number of stores after t years

S0 is the initial number of stores

If a chain of retail computer stores opened 2 stores in its first year of operation then at t = 1, S(t) = 2. Substitute into the equation;

2 = S0e^k(1)

2 = S0e^k .... 1

Also if after 8 years of operation, the chain consisted of 206 stores, this means at t = 8, S(t) = 206. Substitute into the equation;

206 = S0e^k(1)

206 = S0e^8k .... 2

Next is to calculate the value of k

Divide equation 2 by 1;

`(206)/(2) = (S0e^(8k) )/(S0e^k )\\103 = e^(7k)\\apply \ ln \ to \ both \ sides\\ln103 = lne^(7k)\\ln103 = 7k\\k = (ln103)/(7)\\k = (4.6347)/(7) \\k = 0.6621`

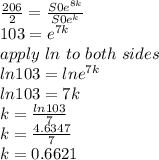
Hence the value of k to the nearest hundredth is 0.66