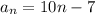Question

NO LINKS!!! NOT A MULTIPLE CHOICE!!

8. a. Finish the table

b. Name the type of sequence​

Answer 1

To determine the type of sequence, calculate the differences between the terms:

`33 \underset{+10}{\longrightarrow} 43 \underset{+10}{\longrightarrow} 53`

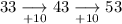
Therefore, this is an arithmetic sequence, as the difference between the terms is constant → the common difference is 10.

General form of an arithmetic sequence:

`a_n=a+(n-1)d`

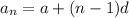
where:

• 
  `a_n` is the nth term
• a is the first term
• d is the common difference between terms

To find the first term, substitute the known values into the formula and solve for a:

`\begin{aligned}\implies a_4=a+(4-1)10 & =33\\a+30 & = 33\\a & = 3\end{aligned}`

Therefore:

`\implies a_n=3+(n-1)10`

`\implies a_n=3+10n-10`

`\implies a_n=10n-7`

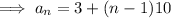
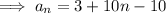
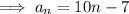
Finding the 7th and 8th terms:

`\implies a_7=10(7)-7=63`

`\implies a_8=10(8)-7=73`

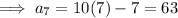
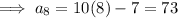
Part (a)

`\large \begin{array} c \cline{1-6} n & 4 & 5 & 6 & 7 & 8 \\\cline{1-6} t(n) & 33 & 43 & 53 & 63 & 73 \\\cline{1-6}\end{array}`

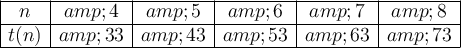
Part (b)

Arithmetic sequence

Part (c)

`a_n=10n-7`