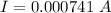Complete Question
A flat loop of wire consisting of a single turn of cross-sectional area 8.00 cm2 is perpendicular to a magnetic field that increases uniformly in magnitude from 0.500 T to 1.60 T in 0.99 s. What is the resulting induced current if the loop has a resistance of
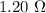
Answer:
The current is
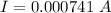
Step-by-step explanation:
From the question we are told that
The area is

The initial magnetic field at
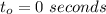 is
is
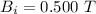
The magnetic field at
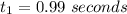 is
is
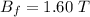
The resistance is
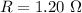
Generally the induced emf is mathematically represented as
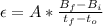
=>
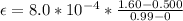
=>
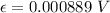
Generally the current induced is mathematically represented as
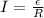
=>
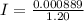
=>