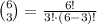Answer:
(a) 1,902,231,808,400
(b) 84
(c) 20
Explanation:
In mathematics, the procedure to select k items from n distinct items, without replacement, is known as combinations.
The formula to compute the combinations of k items from n is given by the formula:
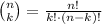
(a)
Compute the number of ways to select 9 applicants from 100 as follows:


(b)
Compute the number of ways to select 6 people from 9 as follows:
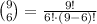
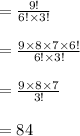
(c)
Compute the number of ways to select top 3 candidates from 6 as follows: