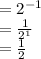Question

Describe how (2 ^ 3)(2 ^ - 4) can be simplified . Multiply the bases and add the exponents. Then find the reciprocal and change the sign of the exponent . The same base and add the exponents . Then multiply by - 1 . The base and multiply the exponents . Then multiply by -1 Add the exponents and keep the same base Then find the reciprocal and change the sign of the exponent .

Answer 1

D

Explanation:

Answer 2

Add the exponents and keep the same base Then find the reciprocal and change the sign of the exponent .

Explanation:

Given the expression (2^3)(2^- 4), we will apply the law of indices below to solve the equation;

`a^m * a^n = a^(m+n)\\a^(-m) =(1)/(a^m)`

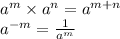
Applying this on the given expression;

`(2 ^ 3)(2 ^(-4))`

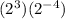
Step 1: Add the exponents and keep the same base as shown;

`= (2 ^ 3)(2 ^(-4))\\\\= 2^(3+(-4))\\\\ = 2^(3-4)\\\\= 2^(-1)`

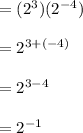
Step 2: Find the reciprocal and change the sign of the exponent

`= 2^(-1) \\= (1)/(2^1)\\= (1)/(2)`