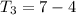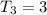Answer:
1)
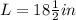

2)
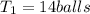
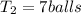
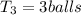
Explanation:
In order to solve this problem, we need to build the equations we need. Since there are two values we want to figure out (length and width) we will then need two equations to solve simultaneously.
First, the problem tells us that the perimeter is 55 1/2 in, which can be rewritten as an improper fraction:

Next, we also know the perimeter of a rectangle is found by using the following formula:
P=2L+2W
where L is the length of the rectangle and W is its width.
So our first equation will look like this:

Next, the problem tells us that the width of the rectangle is twice its width, so our second equation will look like this:
L=2W
which can be substituted into our first equation:
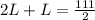
Now, we can solve this for L, so we get:
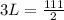
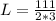
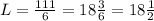
so we can now use this information to find its width:
L=2W
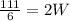
so


2)
When solving this problem it is a good idea to split it into little chunks of information. The first sentence says:
"... "teacher 1" shoots twice as many airballs as "teacher 2"."
This can be translated as an equation like this:

The next sentence says:
""teacher 3" shoots 4 airballs less than "teacher 2"."
This can be written as an equation like this:
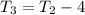
and finally, the problem states: "... they shot 24 airballs together,..."
This can be written as an equation like this:
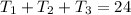
so now we can do substitutions. We can take the first and second equations and write them into the third equation so we get:
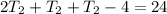
so now we can solve this equation for
 , so we get:
, so we get:
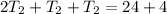
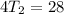


and once we got this answer, we can find the remaining two answers:

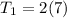
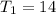
and
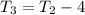
so we get: