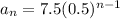Question

NO LINKS!!! NOT MULTIPLE CHOICE!!

9. a Finish the table


b. Name the type of sequence

c. Find the equation of the sequence
​

Answer 1

0.9375, 0.46875

I’m not sure what sequence it is, but it might be geometric progression

the equation is t(n)= n / 2

Explanation:

hope this helps !

Answer 2

Number Sequence: a set of numbers that follow a pattern or a rule, where each number in the sequence is called a term.

Arithmetic Sequence: has a constant difference between each term, so the difference between each term is the same.

Geometric Sequence: has a constant ratio (multiplier) between each term, so each term is multiplied by the same number.

To determine the type of sequence, calculate the differences between the terms:

`7.5 \underset{-3.75}{\longrightarrow} 3.75 \underset{-1.875}{\longrightarrow} 1.875`

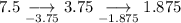
Therefore, this is not an arithmetic sequence, as the difference between the terms is not the same.

General form of a geometric sequence:

`a_n=ar^(n-1)`

(where a is the first term and r is the common ratio)

To find the common ratio r, divide consecutive terms:

`\implies r=(a_2)/(a_1)=(3.75)/(7.5)=0.5`

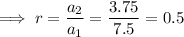
Therefore:

`a_n=7.5(0.5)^(n-1)`

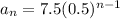
Finding the 4th and 5th terms:

`\implies a_4=7.5(0.5)^(4-1)=0.9375`

`\implies a_5=7.5(0.5)^(5-1)=0.46875`

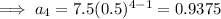
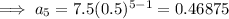
Part (a)

`\large \begin{array} c \cline{1-6} n & 1 & 2 & 3 & 4 & 5 \\\cline{1-6} t(n) & 7.5 & 3.75 & 1.875 & 0.9375 & 0.46875 \\\cline{1-6}\end{array}`

Part (b)

Geometric sequence

Part (c)

`a_n=7.5(0.5)^(n-1)`