Question

Direction: Complete the table below by checking the description of roots and solve

the value of discriminant b2 - 4ac.
Description of roots
Value of
discriminant
b2 - 4ac
Equation
Equal
Not
Equal
Real
Non Real
1.4x2 + 4x + 1 = 0​



pls,, help me

Answer 1

The polynomial
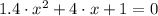`1.4\cdot x^(2)+4\cdot x +1=0` have real roots.

Explanation:

The second-order polynomial required to be analyzed is
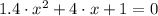`1.4\cdot x^(2)+4\cdot x +1=0`. From Algebra we remember that second-order polynomials of the form
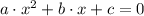`a\cdot x^(2)+b\cdot x +c =0` can be solved by the Quadratic Formula, of which we can determined if their roots are either real or complex by the ressource of the discriminant, defined as:

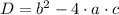`D=b^(2)-4\cdot a\cdot c` (1)

Roots are real if and only if
`D \ge 0`, otherwise roots are complex.

If we know that
`a = 1.4`,
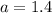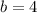`b = 4` and
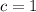`c = 1`, then the value of the discriminant is:

`D = 4^(2)-4\cdot (1.4)\cdot (1)`

`D = 10.4`

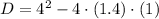
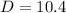
The polynomial
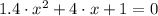`1.4\cdot x^(2)+4\cdot x +1=0` have real roots.