Question

I added pics cause it’s 2 in the morning.. I’m having back pain, thigh pain, cramps EVERYWHERE.. headache and just finished babysitting my baby brother.. help a gurl out please ( yes I have been copying and pasting)

Answer 1

Conner's work is correct

Explanation:

Operations With Exponents

We need to use the rule to find the product of two or more exponential expressions:

`x^m\cdot x^n\cdot x^p = x^(m+n+p)`

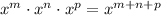
We need to multiply:

`(3^5 6^8)(3^9 6^(10))`

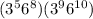
Base 3 is treated independently from base 6, so we have two groups of operations:

`(3^5 6^8)(3^9 6^(10))=3^(5+9) 6^(8+10)`

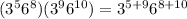
Adding the exponents:

`(3^5 6^8)(3^9 6^(10))=3^(14) 6^(18)`

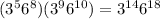
Thus, Conner's work is correct