Question

HELP ME ASAP 50 POINTS​

Answer 1

See below ~

Explanation:

Let's get started!

Part (a) :

Statement 1 : ∠A = ∠E = 90° (indicated in diagram)

Statement 2 : ∠C = ∠C (common angle)

⇒ ΔABC ~ ΔBDC (AA similarity)

Part (b) :

Now that we have proved the triangles to be similar, we can take their corresponding sides in proportion.

⇒
`(EC)/(AC) = (ED)/(AB)`

⇒
`(160)/(160+50) = (120)/(AB)`

⇒
`(16)/(21) = (120)/(AB)`

⇒
`AB = (120*21)/(16)`

⇒
`AB = (2520)/(16)`

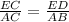
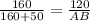
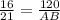
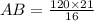
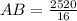
⇒ AB = 157.5

Answer 2

Let's use Thales theorem

• AC/AB=CE/DE
• 50+160/AB=160/120
• 210/AB=4/3
• 4AB=630
• AB=630/4
• AB=157(Approx)