Answer: 0.167
Explanation:
Given: Total batteries = 10
Batteries that are still working = 6
Number of ways to pick 3 working batteries =
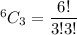
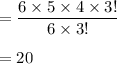
Number of ways of pick 3 batteries out of 10 =

Required probability =
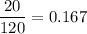
Hence, the probability that all of the first 3 she chooses will work = 0.167