Answer:
1 time
Explanation:
Given numbers are 54 and 36.
The greatest common divisor of 54 and 36 = 18
So,
 .
.
The least common multiple of 54 and 36 = 108
So,
 .
.
As 54 is replaced by
 and 36 is replaced by
and 36 is replaced by
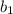 , so after applying the given procedure, the new number is
, so after applying the given procedure, the new number is
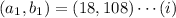
Now, apply the same procedure, to get
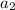 and
and
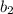 .
.
The greatest common divisor of 18 and 108 = 18
So,
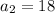 .
.
The least common multiple of 18 and 108 = 108
So,
 .
.
As
 is replaced by
is replaced by
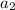 and
and
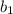 is replaced by
is replaced by
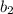 , so after applying the given procedure, the new number is
, so after applying the given procedure, the new number is
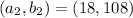 which is the same as in equation (i)
which is the same as in equation (i)
Hence, after applying the procedure 1 time after
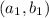 , the obtained number
, the obtained number
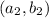 is the same as
is the same as
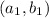 .
.